Continuation du spectre
Exemple 1
La transformée de Fourier du signal échantillonné idéal peut prouver que le spectre du signal échantillonné idéal est l'extension périodique du spectre du signal continu. La période de répétition est Ws (fréquence d'échantillonnage), c'est-à-dire
Exemple 2
où est le spectre de fréquence du signal d'échantillonnage idéal, qui est la transformée de Fourier du signal continu. Évidemment, c'est une fonction continue de la fréquence .
Fréquence numérique de coin.
Théorème d'échantillonnage
Si le signal xa(t) est un signal à bande réelle limitée et que le spectre de fréquence le plus élevé ne dépasse pas Ws/2, c'est
le théorème d'échantillonnage
Ensuite, dans le spectre d'échantillonnage idéal, le spectre en bande de base et le spectre de modulation harmonique de chaque ordre ne se chevauchent pas. Un filtre passe-bas idéal avec une bande passante de Ws/2 peut filtrer le spectre de modulation harmonique de chaque ordre. , Pour conserver le spectre de bande de base non déformé, afin de restaurer le signal continu d'origine sans distorsion.
mec
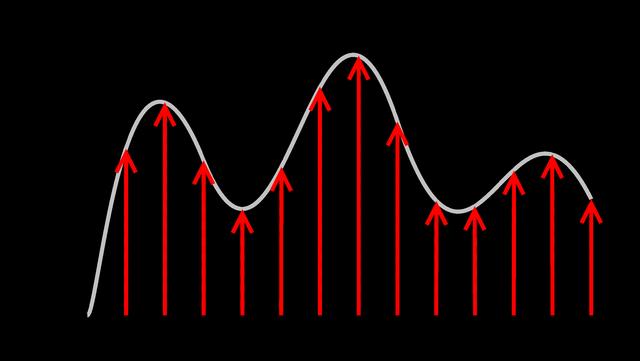
Si le spectre de fréquence le plus élevé du signal dépasse Ws/2, alors dans le spectre échantillonné idéal, les spectres de modulation de chaque instant se chevaucheront et il y aura un phénomène de « mélange » du spectre, comme le montre la figure 1.4. le diagramme de repliement du spectre. Par souci de concision, le diagramme de repliement du spectre de la figure 1.4 traite Xa(jW) comme un scalaire. Généralement, Xa(jW) est un nombre complexe, et le chevauchement est également l'addition de nombres complexes. Lorsqu'un repliement de spectre se produit, il est généralement impossible de filtrer le spectre en bande de base sans distorsion, et le signal récupéré par le filtrage en bande de base sera déformé.
Par conséquent, la moitié de la fréquence d'échantillonnage, Ws/2, est appelée fréquence de repliement. C'est comme un miroir. Lorsque le spectre du signal le dépasse, il sera replié, provoquant une confusion du spectre.
Théorème d'échantillonnage de Nyquist : Afin de restituer le signal réel sans distorsion après échantillonnage, la fréquence d'échantillonnage doit être supérieure au double de la fréquence la plus élevée du signal, soit Ωs≥2Ωmax.
Dans le travail réel, afin d'éviter le repliement du spectre, la fréquence d'échantillonnage est toujours sélectionnée pour être supérieure au double de la fréquence la plus élevée Wmax du signal, telle que Ws>(3~5)Wmax. Dans le même temps, afin d'empêcher le spectre parasite supérieur à la fréquence de repliement d'entrer dans l'échantillonneur et de provoquer un repliement du spectre, un filtre passe-bas protecteur (filtre anti-crénelage) est souvent ajouté avant l'échantillonneur pour éviter les composantes de fréquence plus élevées. que WS/2 d'entrer .
3) Transformée de Laplace du signal échantillonné
Après un échantillonnage idéal, la transformée de Laplace du signal est périodiquement prolongée le long de l'axe imaginaire sur le plan S, c'est-à-dire l'axe imaginaire L'axe est une fonction périodique.
Dans le domaine du traitement de l'information, un signal d'échantillonnage signifie que le signal analogique est d'abord échantillonné par un échantillonneur à un certain intervalle de temps pour obtenir un signal discret dans le temps.
Ces signaux sont également discrétisés numériquement par le convertisseur analogique-numérique (CAN), de manière à obtenir un signal numérique à la fois numériquement et temporellement discret.
L'ensemble du processus est appelé échantillonnage. Dans de nombreux cas, « échantillonnage » fait référence au processus consistant à combiner l'échantillonnage et la quantification.
L'échantillonnage, encore appelé échantillonnage, est la discrétisation du signal dans le temps, c'est-à-dire que la valeur instantanée du signal analogique x(t) est prise point par point selon un certain intervalle de temps △t. Il est réalisé en multipliant l'impulsion d'échantillonnage et le signal analogique.
Sélection de l'intervalle d'échantillonnage et confusion du signal : Pour échantillonner un signal analogique, déterminez d'abord l'intervalle d'échantillonnage. Comment choisir ? Cela implique de nombreux facteurs techniques qui doivent être pris en compte. De manière générale, plus la fréquence d'échantillonnage est élevée, plus le nombre de points d'échantillonnage est dense et plus le signal discret résultant est proche du signal d'origine. Cependant, aussi
Une fréquence d'échantillonnage élevée n'est pas recommandée. Pour les signaux de longueur fixe (T), trop de volume de données (N=T/△t) est collecté, ce qui ajoute un travail de calcul inutile à l'ordinateur Si la quantité de données (N) est limitée, le temps d'échantillonnage est trop court, ce qui entraînera l'exclusion de certaines informations de données. Échantillonnage
La fréquence est trop basse et l'intervalle du point d'échantillonnage est trop éloigné, le signal discret n'est pas suffisant pour refléter les caractéristiques de la forme d'onde du signal d'origine et le signal ne peut pas être restauré, ce qui provoque une confusion du signal.
Intuitivement parlant, le repliement du signal consiste à confondre des signaux qui devraient être des signaux haute fréquence avec des signaux basse fréquence.
