Concepts connexes
Une fonction
En mathématiques, la fonction itérative est l'objet d'une étude approfondie dans le système fractal et dynamique. La fonction itérative est une fonction qui se compose de façon répétitive.
Modèle
Le modèle itératif est un modèle de cycle recommandé par RUP (Rational Unified Process, processus de développement de logiciel unifié, processus de logiciel unifié).
Algorithme
L'algorithme itératif est une méthode de base pour résoudre les problèmes avec les ordinateurs.
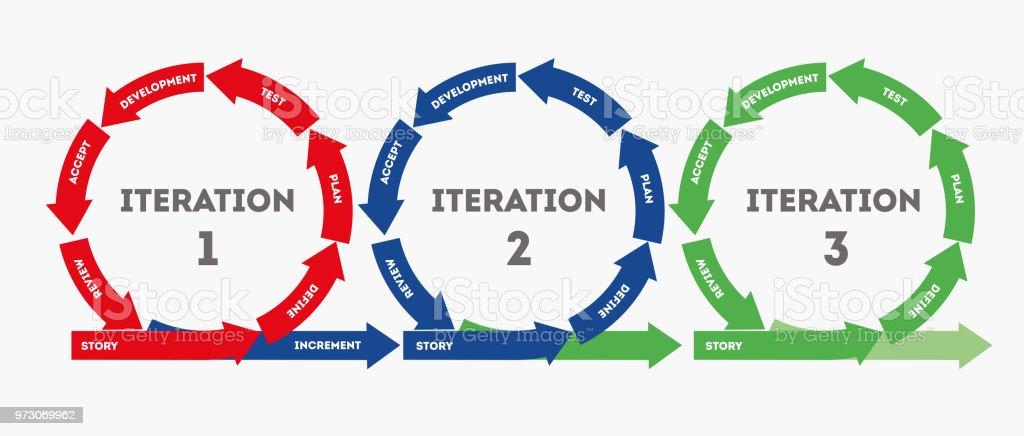
Modèle RUP
Compréhension
Si vous pensez que cette explication est difficile à comprendre, vous pouvez y penser comme ceci :
Nous développons un produit, sinon c'est compliqué et adopterons le modèle de la cascade. En termes simples, il s'agit de définir d'abord les exigences, puis de construire le cadre, puis d'écrire le code, puis de tester et enfin de publier un produit.
De cette façon, quelques mois se sont écoulés et personne ne peut voir un produit avant le dernier jour de sortie.
Cette méthode présente des lacunes évidentes. Si vous n'êtes pas très précis dans l'évaluation des besoins des utilisateurs - c'est un problème très courant, et ce n'est pas rare - vous avez travaillé pendant quelques mois, voire quelques années, lorsque vous montrez vos produits aux clients, les clients sont souvent surpris.
Méthode
Theiterationmethodisdifferent.Ifthisproductrequires6monthsdelivery, Iwillcomeupwithaproductinthefirstmonth.Ofcourse, thisTheproductwillbeveryimperfect, therewillbemanyfunctionsthathavenotbeenadded, therearemanybugs, anditisnotstable, butafterthecustomerreadsit, theywillputforwardmoredetailedsuggestionsformodification.Inthisway, youwillknowhowfaryouarefromthecustomer'sneeds.AfterIgohome, Ispendanothermonthtofurtherimproveonthebasisofthedemandanalysis, frameworkdesign, code, test, etc.Imadelastmonth, andthencomeupwithamorecompleteproducttoshowcustomersandletthemComments.
De cette façon, mon produit peut s'approcher progressivement des exigences du client en termes de fonctionnalité et de qualité.
Avantages
Cette méthode est très bonne, mais elle a aussi ses propres lacunes, à savoir que le cycle est long et le coût est élevé. Lorsqu'il s'agit de grands projets et de projets à haut risque, comme le système de contrôle d'une navette spatiale, le coût de l'itération est beaucoup plus faible que le risque d'échec du projet. Cette méthode présente des avantages évidents.
Si vous développez un petit SIM pour votre propre unité, et que vous connaissez bien vos besoins, la période de construction ne prendra qu'un mois, et l'itération est un peu comme un marteau. Il s'agit toujours d'une cascade.
Algorithme de base
Certains manuels étrangers, comme la version chinoise de la quatrième édition de " C++ Primer ", se traduiront par itération en itération.
En Java, Itératif sert uniquement à parcourir la collection, et ne donne pas la possibilité de contenir des objets.
L'utilisation d'algorithmes itératifs pour résoudre des problèmes nécessite les trois aspects suivants :
Déterminer les variables
Parmi les problèmes qui peuvent être résolus par des algorithmes itératifs, il existe au moins une variable qui repousse directement ou indirectement de nouvelles valeurs à partir d'anciennes valeurs, et cette variable est une variable d'itération.
Établir une expression relationnelle
L'expression relationnelle dite itérative fait référence à une formule (ou relation) permettant de déduire la valeur suivante d'une variable de la valeur précédente de la variable.
Contrôle de processus
Whendoestheiterativeprocessend Thisisaquestionthatmustbeconsideredwhenwritinganiterativeprogram.Theiterativeprocesscannotberepeatedendlessly.Thecontroloftheiterativeprocesscanusuallybedividedintotwosituations: oneisthattherequirednumberofiterationsisacertainvalueandcanbecalculated; theotheristhattherequirednumberofiterationscannotbedetermined.Fortheformercase, afixednumberofloopscanbeconstructedtocontroltheiterativeprocess, forthelattercase, itisnecessarytofurtheranalyzetheconditionsusedtoendtheiterativeprocess?.
Exemple 1 : Séquence de Fibonacci
C'est-à-dire une telle séquence : 0,1,1,2,3,5,8,13......,en mathématiques,la séquence de nombres est définie comme :
F(0)=0,F(1)=1;F(n)=F(n-1)+F(n-2)(n≥2,n∈N*).
Généralement, cette séquence peut être implémentée de manière récursive.
intfab(intn)
{si(n<3)
{retour1;}
autre
{intfirst=1,second=1,temp=0;
pour(inti=0;je
{temp=premier+seconde ;
premier=deuxième ;
seconde=temp;}
retourtemp;
p>}
}
Exemple1 :Unenouvelleracedelapinaétéintroduitedansuneferme d'élevage.
Analyse : Ce problème de récurrence est typique. Supposons que le nombre de lapins du premier mois d'u1, le nombre de lapins du deuxième mois d'u 2 et le nombre de lapins du troisième mois d'u 3...
Le fragment suivant :
u1=1,u2=u1+u1×1=2,u3=u2+u2×1=4,……
Selon cette règle, la formule de récurrence suivante peut être conclue :
Le fragment suivant :
un=(un-1)×2(n≥2)*①
Correspondantàunetun-1,définirdeuxvariablesd'itérationyetx,laformulederécurrencecidessuspeutêtreconvertiedanslarelationitérativesuivante :
Le fragment suivant :
y=x*2
x=y
Laissez l'ordinateur répéter cette relation d'itération 11 fois pour calculer le nombre de lapins au 12e mois. Le programme de référence est le suivant :
L'extrait ci-dessous :
cls
x=1
fori=2à12
y=x*2
x=y
ensuite je
imprimé
finir
Exemple2:Amoebareproduitd'unefaçonsimpledefractionner,chaque foisse fractionne,cela prend3minutes.Mettezplusieursamibesdansunrécipientpleindenutrimentginsengliquid,etaprès45minuteslerécipientestremplid'amibe.On sait quelerécipientpeutcontenirjusqu'à20amibes.
Analyse: Accordingtothemeaningofthequestion, amoebasplitsevery3minutes, thenputtheamoebaintothecontaineratthebeginning, andfillthecontainerafter45minutes, youneedtosplit45 / 3 = 15Second-rate.And "thecontainercanhold220amoebaatmost", thatis, thenumberofamoebaobtainedafter15splitsis220.Thetitleasksustocalculatethenumberofamoebabeforethesplit.Wemightaswellusethebackwarddeductionmethod, from2to20afterthe15thsplit, backtothenumberbeforethe15thsplit (thatis, afterthe14thsplit), andthenFurtherinferthenumbersafterthe13thsplit, afterthe12thsplit, ... beforethefirstsplit.
Supposons que le nombre avant le premier fractionnement x0, le nombre après le premier fractionnement x1, le nombre après le deuxième fractionnement x2,...le 15ème fractionnement
Les fragments suivants sont cités :
x14=x15/2,x13=x14/2,...xn-1=xn/2(n≥1)
Étant donné que le nombre x15 après la 15e division est connu, si la variable d'itération est définie par x, la formule ci-dessus peut être convertie en la formule itérative suivante :
x=x/2(lavaleurinitialedexestlenombreaprèsle15èmesplit :220)
Que cette formule itérative soit répétée 15 fois, vous pouvez déduire le nombre d'amibes avant la première division.
Le fragment suivant :
cls
x=2^20
fori=1to15
x=x/2
ensuite je
imprimerx
finir
Exemple3 : Vérifiez la conjecture de Kakutani. L'émathématicien japonais Shizuo Kakutan a découvert un phénomène étrange lors de l'étude des nombres naturels :
Conditions préalables : Ecrire un programme, saisir un nombre n naturel à partir du clavier et imprimer l'ensemble du processus n après un nombre fini d'opérations, qui devient finalement un nombre naturel 1.
Analyse : définir la variable d'itération comme n. Selon le contenu de la conjecture de Kakutani, la relation itérative dans deux cas peut être obtenue : lorsqu'il est un nombre pair, n = n/2 ; lorsqu'il est un nombre impair, n = n * 3+1. Pour le décrire en langage QBASIC est :
Le fragment suivant :
si c'est un nombre pairalors
n=n/2
autre
n=n*3+1
fin si
Thisistheiterativeprocessthatneedstoberepeatedbythecomputer.Howmanytimesdoesthisiterativeprocessneedtoberepeatedtomaketheiterativevariableneventuallybecomeanaturalnumber1, whichissomethingwecannotcalculate.Therefore, itisnecessarytofurtherdeterminetheconditionsusedtoendtheiterativeprocess.Aftercarefulanalysisofthesubjectrequirements, itisnotdifficulttoseethatforanygivennaturalnumbern, aslongasthenaturalnumber1canbeobtainedafterafinitenumberofoperations, theverificationworkhasbeencompleted.Therefore, theconditionusedtoendtheiterativeprocesscanbedefinedas: n = 1.Thereferenceprogramisasfollows:
Le fragment suivant :
cls
input"Pleaseinputn=";n
jusqu'à 1
ifnmod2=0alors
remIfnisunnombre pair,appellaformule itérative=n/2
n=n/2
imprimer"—";n;
autre
n=n*3+1
imprimer"—";n;
fin si
boucler
finir
Exemple d'application
Méthode itérative désutiliséeUne méthode de conception d'algorithmes couramment utilisée pour trouver des racines d'équations approximatives.
Choisissezlaracineapproximatived'uneéquationetaffectezla àVariablex0 ;
Stockerlavaleurdex0invariablex1,puiscalculereg(x1),etstockerlavariablerésultantex0;
⑶Lorsqueladifférenceentrex0etx1Lorsquelavaleurabsolueesttoujourssupérieureàl'exigencedeprécisionspécifiée,répétezlecalculàl'étape(2).
Si l'équation a des racines et que la séquence de racines approximative calculée par la méthode ci-dessus converge, le x0 obtenu par la méthode ci-dessus n'est pas considéré comme la racine de l'équation.
[Algorithme] Méthode itérative pour trouver la racine de l'équation
Le fragment suivant :
{x0=initialapproximationRoot;
faire{
x1=x0 ;
x0=g(x1);/*Calculer unenouvelleracineapproximativeselonuneéquationspécifique*/
}while(fabs(x0-x1)>Epsilon);
printf("La racine approximative de l'équation est %f\n",x0) ;
}
Les algorithmes itératifs sont également souvent utilisés pour trouver les racines des équations.
X=(x0,x1,…,xn-1)
Définirl'équationLegroupeest :
xi=gi(X)(I=0,1,...,n-1)
L'algorithme itératif pour trouver la racine du groupe d'équations peut être décrit comme suit :
p>[Algorithme]Méthode itérativepourtrouverlesracinesdusystèmed'équations
Le fragment suivant :
{pour(i=0;i
x=racine approximative initiale ;
faire{
pour(i=0;i
y=x ;
pour(i=0;i
x=gi(X);
pour(delta=0.0,i=0;i
if(fabs(yx)>delta)delta=fabs(yx);
} while(delta>Epsilon);
pour(i=0;i
printf("variablexLa racine approximativede[%d]est%f",I,x);
printf("\n");
}
Utilisez l'itération Faites attention aux deux situations possibles suivantes lors de la recherche des racines :
⑴Sil'équation n'a pas de solution, la séquence de racines approximative calculée par l'algorithme ne convergera pas et le processus d'itération deviendra une boucle sans fin. Avant l'algorithme itératif, vérifiez si l'équation a une solution et limitez le nombre d'itérations dans le programme ;
⑵Bien que l'équation ait une solution, la formule itérative n'est pas correctement sélectionnée ou la racine initiale approximative de l'itération n'est pas raisonnable, elle entraînera également l'échec de l'itération.
①Nisthenumberofrabbits,Misthemonth(N+N*1)^M-1=2N^M-1(Note)
